The New 60/40
I want to share a brilliant idea and a great example from the You’re Looking at the Wrong Number post at the GestaltU blog. Today, I will focus on the section of this post that outlines simple steps to improve a typical 60/40 stock/bond portfolio by using risk allocation instead of dollar allocation, and targeting constant portfolio volatility.
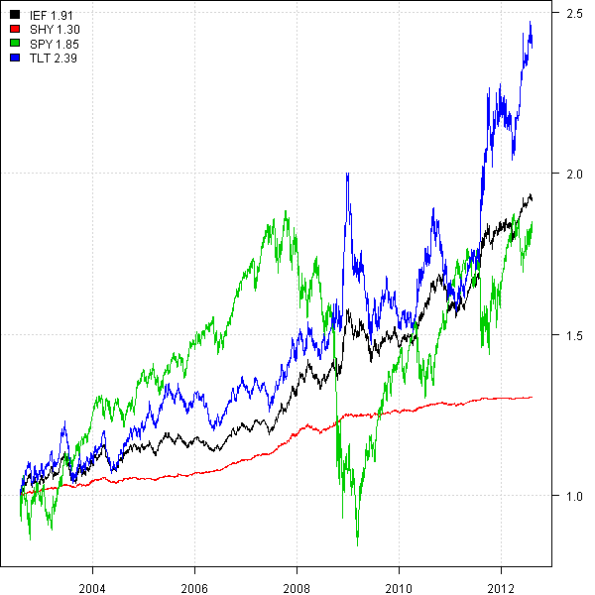
I will use SPY (S&P 500) as a proxy for a stock allocation and TLT (20 Year Treasuries) as a proxy for a bond allocation. Let’s start by loading historical prices for SPY and a few fixed income ETF’s using the Systematic Investor Toolbox:
###############################################################################
# Load Systematic Investor Toolbox (SIT)
# https://systematicinvestor.wordpress.com/systematic-investor-toolbox/
###############################################################################
setInternet2(TRUE)
con = gzcon(url('http://www.systematicportfolio.com/sit.gz', 'rb'))
source(con)
close(con)
#*****************************************************************
# Load historical data
#******************************************************************
load.packages('quantmod')
tickers = spl('SHY,IEF,TLT,SPY')
data.all <- new.env()
getSymbols(tickers, src = 'yahoo', from = '1990-01-01', env = data.all, auto.assign = T)
for(i in ls(data.all)) data.all[[i]] = adjustOHLC(data.all[[i]], use.Adjusted=T)
bt.prep(data.all, align='remove.na')
prices = data.all$prices
n = ncol(prices)
nperiods = nrow(prices)
# normalize all prices and plot them
prices = prices/ matrix(first(prices), nr=nperiods, nc=n, byrow=T)
plota.matplot(prices)
The fixed income ETFs are not as safe as you might have been expected. The SHY (Barclays 1-3 Year Treasury Bond Fund) is consistently up with out large draw-downs. However, both IEF (Barclays 7-10 Year Treasury Bond Fund) and TLT (Barclays 20 Year Treasury Bond Fund) do go through periods of loosing money.
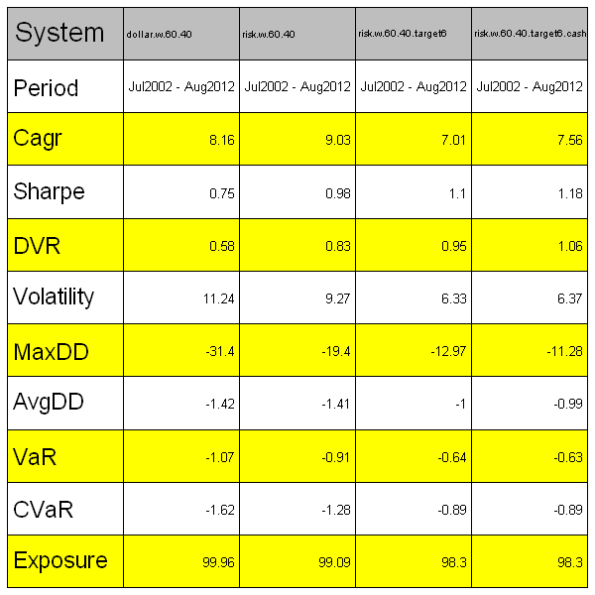
Next let’s build a traditional dollar weighted 60/40 stock/bond portfolio and risk weighted version:
#***************************************************************** # Load historical data #****************************************************************** data <- new.env() data$stock = data.all$SPY data$bond = data.all$TLT bt.prep(data, align='remove.na') #***************************************************************** # Code Strategies #****************************************************************** # all bonds began trading at 2002-07-31 prices = data$prices n = ncol(prices) nperiods = nrow(prices) models = list() period.ends = endpoints(prices, 'months') period.ends = period.ends[period.ends > 0] #***************************************************************** # Traditional, Dollar Weighted 40% Bonds & 60% Stock #****************************************************************** weight.dollar = matrix(c(0.4, 0.6), nr=nperiods, nc=n, byrow=T) data$weight[] = NA data$weight[period.ends,] = weight.dollar[period.ends,] models$dollar.w.60.40 = bt.run.share(data, clean.signal=F) #***************************************************************** # Risk Weighted 40% Bonds & 60% Stock #****************************************************************** ret.log = bt.apply.matrix(prices, ROC, type='continuous') hist.vol = sqrt(252) * bt.apply.matrix(ret.log, runSD, n = 21) weight.risk = weight.dollar / hist.vol weight.risk = weight.risk / rowSums(weight.risk) data$weight[] = NA data$weight[period.ends,] = weight.risk[period.ends,] models$risk.w.60.40 = bt.run.share(data, clean.signal=F)
Next let’s create a risk weighted portfolio with 6% volatility. I will adjust portfolio leverage up/down based on the one month historical volatility to target 6% annual volatility.
#*****************************************************************
# Helper function to adjust portfolio leverage to target given volatility
#******************************************************************
target.vol.strategy <- function(model, weight,
target = 10/100,
lookback.len = 21,
max.portfolio.leverage = 100/100)
{
ret.log.model = ROC(model$equity, type='continuous')
hist.vol.model = sqrt(252) * runSD(ret.log.model, n = lookback.len)
hist.vol.model = as.vector(hist.vol.model)
weight.target = weight * (target / hist.vol.model)
# limit total leverage
rs = rowSums(abs(weight.target))
weight.target = weight.target / iif(rs > max.portfolio.leverage, rs/max.portfolio.leverage, 1)
return(weight.target)
}
#*****************************************************************
# Scale Risk Weighted 40% Bonds & 60% Stock strategy to have 6% volatility
#******************************************************************
data$weight[] = NA
data$weight[period.ends,] = target.vol.strategy(models$risk.w.60.40,
weight.risk, 6/100, 21, 100/100)[period.ends,]
models$risk.w.60.40.target6 = bt.run.share(data, clean.signal=T)
In the last step, I want to invest portfolio cash position into short-term treasuries (SHY) to improve overall performance and create summary reports:
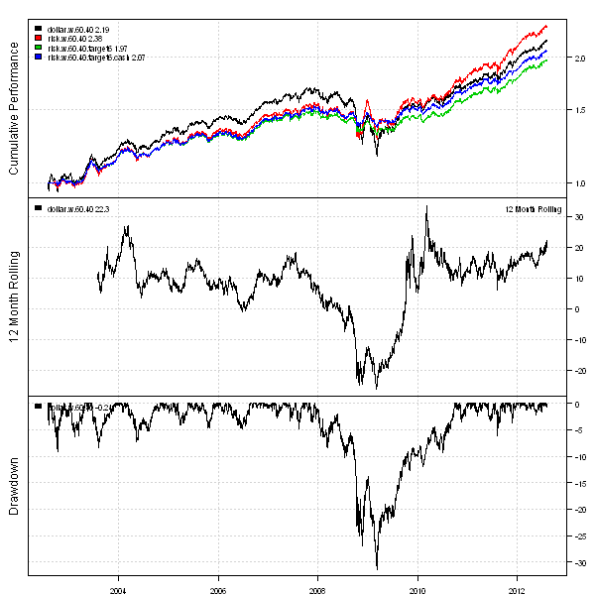
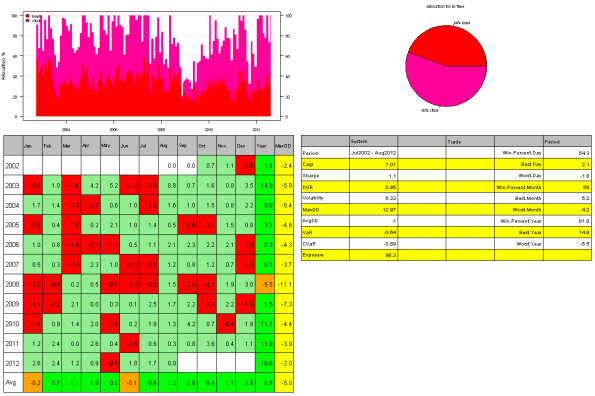
#***************************************************************** # Same, plus invest cash into SHY #****************************************************************** weight = target.vol.strategy(models$risk.w.60.40, weight.risk, 6/100, 21, 100/100) data.all$weight[] = NA data.all$weight$SPY[period.ends,] = weight$stock[period.ends,] data.all$weight$TLT[period.ends,] = weight$bond[period.ends,] cash = 1-rowSums(weight) data.all$weight$SHY[period.ends,] = cash[period.ends] models$risk.w.60.40.target6.cash = bt.run.share(data.all, clean.signal=T) #***************************************************************** # Create Report #****************************************************************** plotbt.strategy.sidebyside(models) plotbt.custom.report.part1(models) plotbt.custom.report.part2(models$risk.w.60.40.target6) plotbt.custom.report.part2(models$risk.w.60.40.target6.cash)
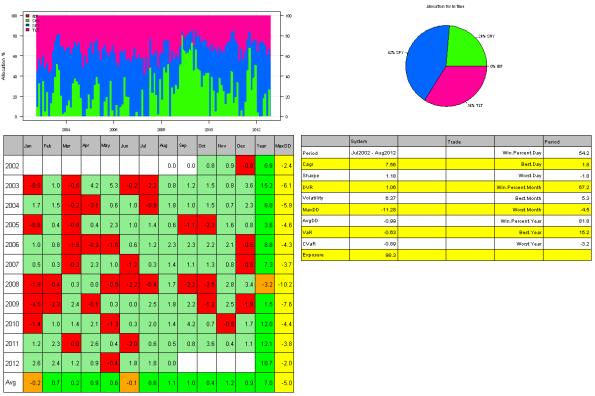
I’m very happy with results: the returns went down a bit, but portfolio risk adjusted performance is up and draw-downs went down from 30% to 12%. The consistent returns are especially important for a retirement portfolio because it allows you to better plan how much money you can withdraw and sustain your fund for a longer term.
To view the complete source code for this example, please have a look at the bt.new.60.40.test() function in bt.test.r at github.

This is great!
great post as usual.
Thanks
Hi – excellent post. One question though. I was under the impression that an equal risk portfolio of stocks and bonds would have an allocation more like 90/10 or 80/20 (bonds vs. stocks). But this analysis seems more weighted to stocks. Can you point out what I am missing? Thanks!
Here are some pointers: